Problem statement

The ‘Largest Rectangle in Histogram’ problem is as follows:

Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

I love this problem as it provides an amazing introduction to problem solving, more specifically, formalizing proofs of why algorithms work. Let’s start with an example:

Let the array of heights be [1, 4, 7, 5, 7]:

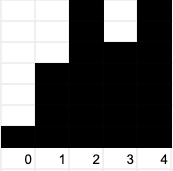
The answer is 16:

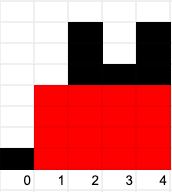
If you have solved this problem before, or just looked at the answer, you may have found it hard to convince yourself why the algorithm works. Fret not, I am here to try formalizing the proof of the algorithm so that you can understand how exactly it works!

The general solution is to keep a monotonically increasing stack of indices

Invariants

We can think of the monotonically increasing property as an invariant that the stack must maintain.

As a refresher, an invariant is a property that is always true across iterations (of a loop) or for all elements in a data structure.

A monotonically increasing stack of indices maintains the following invariants:

Notations

For each index where is the array of heights and . Let be the monotonically increasing stack.

Operations

Many monotonic stack problems involve thinking about two key operations:

1. When to push?
2. When to pop?

Push

When or , then we push to the stack as it maintains the invariant.

Pop

When and , then we pop from the stack, receiving index , and try computing the largest rectangle using as the shortest rectangle.

To calculate the , let . The height of , .

To derive the width of , , we need to find the leftmost and rightmost rectangles that are still . We can label the indices of these rectangles as and .

Otherwise, will no longer be the shortest rectangle. After computing , we can push onto the stack as well.

Solving

Finding the rightmost index

Notice that if and is monotonically increasing, then must be the rightmost tallest rectangle. Formally, the claim can be written as

The above claim implies that can go from to without encountering a shorter rectangle in between.

Suppose that , then it must have caused to be popped off of prior to . However, this causes a contradiction as . Therefore, the claim holds and as a result, .

Finding the leftmost index

Case 1:

If , then by monotonic stack. Thus, the as that implies that the leftmost rectangle that is is itself.

Case 2:

If , then what we want to show is that

To prove this, notice that given that . Also notice that , otherwise, would not be in . This proves the first part of the claim where as can be interchanged with .

Given that as well (otherwise ), then , otherwise, which is a contradiction. That means would have caused the final to be popped from the stack.

Therefore, the claim is proven and we know that as the leftmost rectangle that is is given that by monotonic stack.

Case 3:

If . When this happens there is no leftmost rectangle, so we can set .

Calculating

Therefore, we have found both the rightmost index where , and the leftmost index where , or . The width of is therefore, .

If , then .

If , then .

Implementation

When we implement the algorithm, we see that we naturally derive the ideal stack solution:

def largestRectangleArea(self, heights: List[int]) -> int:
    stack = []
    heights.append(0)
    n = len(heights)
    ans = 0
    for i in range(n):
        while stack and heights[i] < heights[stack[-1]]:
            j = stack.pop()
            h = heights[j]
            w = i if not stack else (i - stack[-1] - 1)
            ans = max(ans, w * h)
        stack.append(i)
    return ans

Conclusion

There you have it! The largest rectangle in histogram algorithm has now been formally proven and the magic numbers have been answered! Of course, when working on these problems during an interview, it is not expected of you to derive these proofs from scratch, but having such an intuition about monotonic stacks help a lot in reasoning with the magic values that are used!